Puzzles and mathematical recreations
Like most Science students, I find fascinating the ingenuity that lies beneath the, in many cases deceptively simple, puzzles and mathematical recreations. Here I have collected some with pointers to many more.
Food for thought
1. The unexpected hanging
A judge sentenced the convict to be hung during the next week. "But,"
he said, "you will not know which day until you are so informed on the
morning of the day of the hanging.
"Well, well," thought the prisoner to himself, "that means I can't be hung! For I can't be hung on Sunday, since if by Saturday night I haven't been hung I will know that the execution will take place on Sunday and, contrary to the judge ruling, I would know it before being told on Sunday morning. But then I can't be hung on Saturday, for if by Friday night I haven't been hung only two days would remain: since hanging is not possible on Sunday, it would have to be on Saturday, but then again I would know it before being told in the morning. And I can rule out the remaining days in exactly the same way!"
Needless to say, he was quite surprised when the hangman arrived on Thursday.
2. How many "F"?
FINISHED FILES ARE THE RESULT OF YEARS OF SCIENTIFIC STUDY COMBINED WITH THE
EXPERIENCE OF YEARS OF WORK BY FAMOUS PROFESSORS.
(The correct answer is 9.)
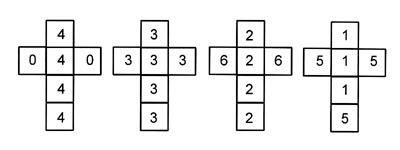
3. Nontransitive dice
Assume you allow someone to pick a die among four and then you select one from the remaining three. Both dice are tossed and the highest number wins; the game is repeated a number of times. Surely it would seem that the game is either fair or favors your opponent, wouldn't it? Truth is, with the set of dice below, you can always pick a die that has a 2/3 probability of winning!
This set of dice was designed by Bradley Efron, a statiscian at Stanford University. Each die beats the one to its right and the fourth beats the first.
4. Random?
Probability, like the above example shows, gives rise to many baffling situations. Here is another: what is the probability that a chord drawn at random inside a circle will be longer than the side of an equilateral triangle inscribed in the circle? The answer, it turns out, depends on the procedure used to draw the random chord; the problem as it stands is not precisely defined. More details can be found in Wikipedia.